图解密码学技术
译者序里译者说本书的中文版引进得有点晚了, 里面的内容还是 2008 年的 特别感谢译者在原作者对书做了修订发行了第 3 版后, 把中文版又修订了一遍 呜呜呜真是太好了, 一定要给译者点赞呀!!!
第 1 部分 密码
1.2.2 发送者, 接收者, 窃听者
发送者 (sender) 发送消息 (message) 给接收者 (receiver) 可能会被窃听者 (eavesdropper) 窃听.
1.2.3 加密与解密
明文 (plaintext) 加密 (encrypt) 之后称为密文 (ciphertext). 解密 (decrypt) 就是将密文恢复成明文的过程.
1.2.4 密码保证了消息的机密性
例子通过运用密码 (cryptography) 技术, 保证了邮件的机密性 (confidentiality).
1.2.5 破译
破译者 (cryptanalyst) 试图将密文还原为明文, 则称为密码破译 (cryptanalysis), 简称为破译, 有时也称为密码分析. 密码学研究者为了研究密码强度, 也经常需要对密码进行破译.
1.3 对称密码与公钥密码
1.3.1 密码算法
用于解决复杂问题的步骤, 通常称为算法 (algorithm). 加密, 解密的算法合在一起统称为密码算法.
1.3.2 密钥
密码算法中的密钥 (key), 则是像 4723951939863623748375084382 这样的一串非常大的数字. (第 3 章详细讲解)
1.3.3 对称密码与公钥密码
- 对称密码 (symmetric cryptography) 是指在加密和解密时使用同一密钥的方式. (多种别名, 如公共密钥密码 (common-key cryptography), 传统密码 (conventional cryptography), 私钥密码 (secret-key cryptography), 共享密钥密码 (shared-key cryptography)) (第 3, 4 章详细讲解)
- 公钥密码 (public-key cryptography) 则是指在加密和解密时使用不同密钥的方式. 又称为非对称密码 (asymmetric cryptography). (第 5 章详细讲解)
1.3.4 混合密码系统
将对称密码和公钥密码结合起来的密码方式称为混合密码系统 (hybrid cryptosystem), 这种系统结合了对称密码和公钥密码两者的优势. (第 6 章详细讲解)
1.4 其他密码技术
密码技术提供的不仅是基于密码的机密性, 还用于检测消息是否被篡改的完整性, 以及用于确认对方是否是本人的认证等.
1.4.1 单向散列函数
为了防止软件被篡改, 有些软件在发布的同时还发布该软件的散列值 (hash, 又称哈希值, 密码校验和 (cryptographic checksum), 指纹 (fingerprint), 消息摘要 (message digest)). 散列值就是用单向散列函数 (one-way hash function) 计算出来的数值. 它所保证的是完整性 (integrity). 可以检测数据是否被篡改过. (第 7 章详细讲解)
1.4.2 消息认证码
消息认证码 (message authentication code) 不仅能够保证完整性, 还能提供消息是否来自所期待的通信对象的认证 (authentication) 机制. (第 8 章详细讲解)
1.4.3 数字签名
数字签名 (digital signature) 是一种能够确保完整性, 提供认证并防止否认 (repudiation) 的密码技术. (第 9 章详细讲解)
1.4.4 伪随机数生成器
伪随机数生成器 (Pseudo Random Number Generator, PRNG) 是一种能够模拟产生随机数列的算法. (第 12 章详细讲解)
1.5 密码学家的工具箱
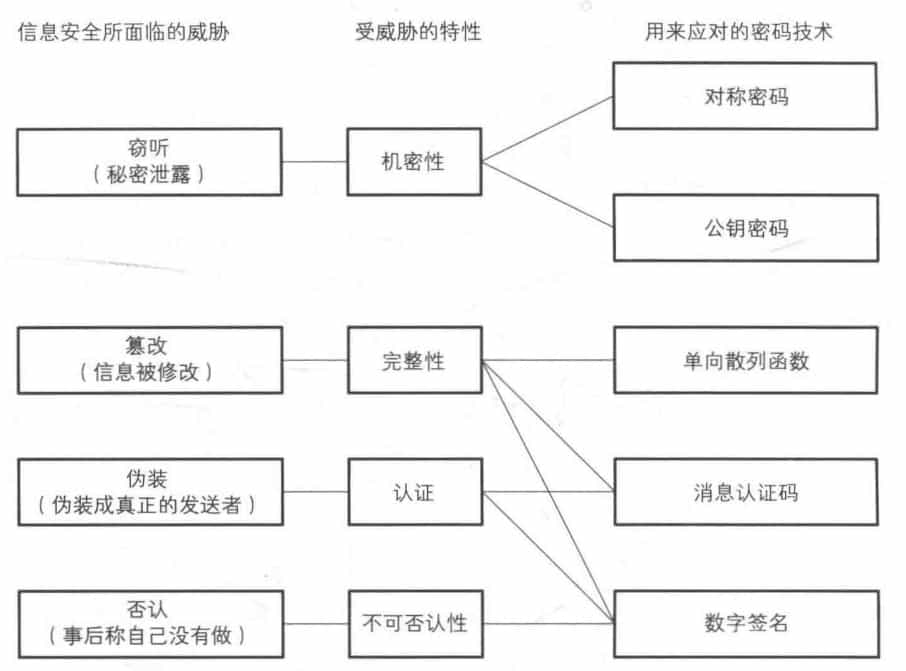
信息安全所面临的威胁与应对这些威胁的密码技术:
1.6 隐写术与数字水印
隐写术 (steganography) 不是让消息内容变得无法解读, 而是能够隐藏消息本身. 数字水印技术就运用了这种方法.
密码隐藏的是内容, 隐写术隐藏的是消息本身. 通过将密码与隐写术相结合, 就可以同时产生两者所各自具备的效果.
1.7 密码与信息安全常识
1.7.1 不要使用保密的密码算法
- 密码算法的秘密早晚会公诸于世
- 开发高强度的密码算法是非常困难的
1.7.2 使用低强度的密码比不进行任何加密更危险
1.7.3 任何密码总有一天都会被破解
严格来说, 绝对不会被破解的密码算法其实是存在的, 这种算法称为一次性密码本 (one-time pad), 但它并不是一种现实可用的算法. (3.4 节详细探讨)
量子密码被认为有可能造就完美的密码技术.
1.7.4 密码只是信息安全的一部分
社会工程学 (social engineering) 与密码强度毫无关系.
复杂的系统就像一根由无数个环节相连组成的链条, 如果用力拉, 链条就会从其中最脆弱的环节处断开. 因此, 系统的强度取决于其中最脆弱的环节的强度. 最脆弱的环节并不是密码, 而是人类自己. 关于这个话题, 作者会在最后一章进行深入的思考.
2 历史上的密码
2.2.1 什么是凯撒密码
恺撒密码 (Caesar cipher) 是通过将明文中所使用的字母表按照一定的字数 “平移” 来进行加密的.
2.2.4 用暴力破解来破译密码
将所有可能的密钥全部尝试一遍, 这种方法称为暴力破解 (brute-force attack). 这种方法的本质是从所有的密钥中找出正确的密钥, 因此又称为穷举搜索 (exhaustive search).
2.3 简单替换密码
将明文中所使用的字母表替换为另一套字母表的密码称为简单替换密码 (simple substitution cipher). 恺撒密码也可以说是简单替换密码的一种.
2.3.4 简单替换密码的密钥空间
恺撒密码可以通过暴力破解来破译, 但简单替换密码很难通过暴力破解来破译.
一种密码能够使用的 “所有密钥的集合” 称为密钥空间 (keyspace), 所有可用密钥的总数就是密钥空间的大小. 密钥空间越大, 暴力破解就越困难.
2.3.5 用频率分析来破译密码
虽然用暴力破解很难破译简单替换密码, 但使用被称为频率分析的密码破译方法, 就能够破译简单替换密码. (作者举了一个例子来让我们体会到破译密码的感觉)
通过例子的破解过程, 可以总结出下列结论:
- 除了高频字母以外, 低频字母也能够成为线索
- 搞清开头和结尾能够成为线索, 搞清单词之间的分隔也能够成为线索
- 密文越长越容易破译
- 同一个字母连续出现能够成为线索 (这是因为在简单替换密码中, 某个字母在替换表中所对应的另一个字母是固定的)
- 破译的速度会越来越快
2.4 Enigma
Enigma 是由德国人于 20 世纪初发明的一种能够进行加密解密操作的机器. Enigma 在德语里是 “谜” 的意思.
2.4.5 每日密码与通信密码
用来加密密钥的密钥, 一般称为密钥加密密钥 (Key Encrypting Key, KEK). 之所以要采用两重加密, 即用通信密码来加密消息, 用每日密码来加密通信密码, 是因为用同一个密钥所加密的密文越多, 破译的线索也会越多, 被破译的危险性也会相应增加.
2.4.6 避免通信错误
在使用 Enigma 的时代, 无线电的质量很差, 可能会发生通信错误. 而通过连续输入两次通信密码, 接收者就可以对通信密码进行校验.
2.4.8 Enigma 的弱点
- 将通信密码连续输入两次并加密
- 通信密码是认为选定的. 应该使用无法预测的随机数来生成. (12章详细探讨)
- 必须派发国防军密码本. 没有就无法使用 Enigma 通信. (第5章详细探讨)
2.4.9 Enigma 的破译
即便知道了 Enigma 的构造, 也还是无法破解 Enigma 的密码, 这是因为 Enigma 的设计并不依赖于 “隐蔽式安全性” (security by obscurity). 即使密码破译者得到了 Enigma 密码机 (相当于密码算法), 只要不知道 Enigma 的设置 (相当于密钥), 就无法破译密码.
2.5 思考
为什么要将密码算法和密钥分开呢?
将密码算法和密钥分开考虑, 就解决了希望重复使用, 但重复使用会增加风险这个难题. 虽然一些历史上的密码技术现在都已经不再使用了, 但是希望重复使用, 但重复使用会增加风险这个难题却依然存在.
每个人都可以拥有相同品牌的锁, 但每个人都有不同的钥匙. 锁的设计是公开的 (锁匠都有带有详细图的书), 而且绝大多数好的设计方案都在公开专利中进行了描述 (但是密钥是秘密的). (布鲁斯 施奈尔: <网络信息安全的真相>)
3 对称密码 (共享密钥密码) (用相同的密钥进行加密和解密)
密码算法有时候会涉及开发者的专利和授权等问题, 因此在使用本书中介绍的密码算法时, 一定要先调查一下该算法的专利和授权信息.
3.3 从文字密码到比特序列密码
3.3.1 编码
计算机的操作对象并不是文字, 而是由 0 和 1 排列而成的比特序列. 执行加密操作的程序, 就是将表示明文的比特序列转换为表示密文的比特序列.
将现实世界中的东西映射为比特序列的操作称为编码 (encoding).
3.3.2 XOR
XOR的全程是 exclusive or, 在中文里叫异或.
由于 XOR 和加法运算很相似, 因此一般用 + 和 ○ 组合而成的符号 🜨 来表示 XOR.
将比特序 A 和比特序 B 进行两次异或运算, 它跟加密, 解密的步骤非常相似.
- 将明文 A 用密钥 B 进行加密, 得到密文 A 🜨 B
- 将密文 A 🜨 B 用密钥 B 进行解密, 得到明文 A
实际上, 只要选择一个合适的 B, 仅仅使用 XOR 就可以实现一个高强度的密码.
3.4 一次性密码本 (绝对不会被破译的密码)
3.4.1 什么是一次性密码本
即便用暴力破解法遍历整个密钥空间, 一次性密码本 (one-time pad) 也绝对无法被破译.
3.4.2 一次性密码本的加解密
它的原理是 “将明文与一串随机的比特序列进行 XOR 运算”. 解密就是加密的反向运算.
3.4.4 一次性密码本是无法破译的
假设对一次性密码本的密文尝试进行暴力破解, 那么总有一天会尝试到和加密时相同的密钥. 但是我们无法判断它是否是正确的明文.
一次性密码本是由维纳 (G.S.Vernam) 于 1917 年提出的, 并获得了专利, 因此又称为维纳密码 (Vernam cipher) (该专利已过有效期). 一次性密码本无法破译这一特性是由香农 (C.E.Shannon) 于 1949 年通过数学方法加以证明的. 一次性密码本是无条件安全的 (unconditionally secure), 在理论上是无法破译的 (theoretically unbreakable).
3.4.5 一次性密码本为什么没有被使用
- 密钥的配送: 如果能够有一种方法将密钥安全地发送出去, 那么岂不是也可以用同样的方法来安全地发送明文了吗?
- 密钥的保存: 我们只是将 “保护明文” 这一命题替换成了 “保护和明文一样长的密钥” 而已.
- 密钥的重用: 如果重用, 过去所有的机密通信内容将全部被破解.
- 密钥的同步: 在通信过程中, 发送者和接收者的密钥比特序列不允许有任何错位, 否则错位的比特后的所有信息都将无法解密.
- 密钥的生成: 一次性密码本中需要生成大量的无重现性的真正随机数 (而不是伪随机数).
综上, 一次性密码本是一种几乎没有实用性的密码. 但其思路孕育出了流密码 (stream cipher). (第 4 章节详细探讨)
3.5 DES
3.5.1 什么是 DES
DES (Data Encryption Standard) 是 1977 年美国联邦信息处理标准 (FIPS) 中所采用的一种对称密码 (FIPS 46-3). DES 一直以来被美国以及其他国家的政府和银行等广泛使用.
随着计算机的进步, 现在 DES 已经能够被短时间内暴力破解, 强度大不如前了, 因此除了用它来解密以前的密文以外, 现在我们不应该再使用 DES 了.
3.5.2 加密和解密
DES 是一种将 64 比特的明文加密成 64 比特的密文的对称密码算法 (这 64 比特的单位称为分组, 以分组为单位进行处理的密码算法称为分组密码 (block cipher)), 但由于每隔 7 比特会设置一个用于错误检查的比特, 因此实质上其密钥长度是 56 比特.
DES 每次只能加密 64 比特的数据, 如果要加密的明文比较长, 就需要对 DES 加密进行迭代 (反复), 而迭代的具体方式就称为模式 (mode). (第 4 章详细探讨)
3.5.3 DES 的结构 (Feistel 网络)
DES 的基本结构是由 Horst Feistel 设计的, 因此也称为 Feistel 网络 (Feistel network), Feistel 结构 (Feistel structure) 或者 Feistel 密码 (Feistel cipher). 其它很多密码算法中也有应用.
// 书中介绍了 Feistel 网络的加密步骤 具体还是看书
Feistel 网络的一些步骤信息:
- 加密的各个步骤称为轮 (round), 整个加密过程就是进行若干次轮的循环. DES 是一种 16 轮循环的 Feistel 网络.
- 子密钥 (subkey) 是其中一轮加密中使用的密钥, 是一个局部密钥.
- 轮函数的作用是根据 “右侧” 和子密钥生成对 “左侧” 进行加密的比特序列, 是密码系统的核心.
Feistel 网络的一些性质:
- 轮数可以任意增加, 都不会发生无法解密的情况.
- 加密时无论使用任何函数作为轮函数都可以正确解密 (无法逆向计算出输入值的函数也可以).
- 加密解密可以用完全相同的结构来实现.
正是由于 Feistel 网络具备如此方便的特性, 它才能够被许多分组密码算法使用. 在后面即将介绍的 AES 最终候选算法的 5 个算法之中, 有 3 个算法 (MARS, RC6, Twofish) 都是使用了 Feistel 网络. 然而, AES 最终选择的 Rijndael 算法却没有使用 Feistel 网络. Rijndael 所使用的结构称为 SPN 结构. (3.8.2 节详细介绍)
3.5.4 差分分析与线性分析
差分分析是一种针对分组密码的分析方法, 思路是 “改变一部分明文并分析密文如何随之改变”. 理论上即便明文只改变一个比特, 密文的比特排序也应该发生彻底的改变. 通过分析密文改变中所产生的偏差, 可以获得破译密码的线索.
线性分析的思路是 “将明文和密文的一些对应比特进行 XOR 并计算其结果为零的概率”. 如果密文具备足够的随机性, 则任选一些明文和密文的对应比特进行 XOR 结果为零的概率应该为 1/2. 如果能够找到大幅偏离 1/2 的部分, 则可以借此获得一些与密钥有关的信息.
差分分析和线性分析都有一个前提, 那就是假设密码破译者可以选择任意明文并得到其加密的结果, 这种攻击方式称为选择明文攻击 (Chosen Plaintext Attack, CPA).
以 AES 为代表的现代分组密码算法, 在设计上已经考虑了针对差分分析和线性分析的安全性.
3.6 三重 DES
DES 已经可以在现实的时间内被暴力破解, 三重 DES 就是出于替代 DES 的分组密码被开发出来的.
三重 DES (triple-DES) 是为了增加 DES 的强度, 将 DES 重复 3 次所得到的一种密码算法. 也称为 TDEA (Triple Data Encryption Algorithm), 通常缩写为 3DES.
明文经过三次 DES 处理才变成密文, 因此三重 DES 的密钥长度是 56 x 3 = 168 比特.
三重 DES 并不是进行三次 DES 加密 (加密 -> 加密 -> 加密), 而是加密 -> 解密 -> 加密的过程. 这个方法是 IBM 公司设计出来的, 目的是为了让三重 DES 能够兼容普通的 DES. (当三重 DES 中所有的密钥都相同时, 三重 DES 就等同于普通的 DES)
- 如果所有密钥都使用相同的比特序列, 则其结果与普通的 DES 是等价的.
- 如果密钥 1 和密钥 3 使用相同的密钥, 而密钥 2 使用不同的密钥, 这种三重 DES 就称为 DES-EDE2.
- 密钥 1, 密钥 2, 密钥 3全部使用不同的比特序列的三重 DES 称为 DES-EDE3.
三重 DES 的解密过程和加密正好相反.
3.6.4 三重 DES 的现状
尽管三重 DES 目前还被银行等机构使用, 但其处理速度不高, 除了特别重视向下兼容的情况下, 很少被用于新的用途.
3.7 AES 的选定过程
对称密码的新标准 (AES)
3.7.1 什么是 AES
AES (Advanced Encryption Standard) 是取代其前任标准 (DES) 而成为新标准的一种对称密码算法. 全世界的企业和密码学家提交了多个对称密码算法作为 AES 的候选, 最终在 2000 年从这些候选算法中选出了一种名为 Rijndael 的对称密码算法, 并将其确定为了 AES.
3.7.2 AES 的选拔过程
// 介绍选拔过程
参加 AES 竞选是有条件的, 这个条件就是: 被评选为 AES 的密码算法必须无条件地免费供全世界使用.
3.8 Rijndael
Rijndael 是由比利时密码学家 Joan Daemen 和 Vincent Rijmen 设计的分组密码算法.
在 AES 的规格中, 分组长度固定为 128比特, 密钥长度只有 128, 192 和 256 比特三种.
3.8.2 Rijndael 的加密和解密
// 介绍过程
3.8.3 Rijndael 的破译
// 介绍破译可能. 不过还是假设, 目前还没出现针对 Rijndael 的有效攻击
3.8.4 应该使用哪种对称密码呢
- DES 不应再用于任何新的用途. 但在某些情况下需要保持与旧版本软件的兼容性.
- 没有理由将三重 DES 用于任何新的用途, 尽管在一些重视兼容性的环境中还会继续使用, 但它会逐渐被 AES 所取代.
- AES 最终候选算法应该可以作为 AES 的备份. 但 NIST 最终选择的标准只有 Rijndael, 并没有官方认可将其他最终候选算法作为备份来使用.
一般来说, 我们不应该使用任何自制的密码算法, 而是应该使用 AES. 因为 AES 在其选定过程中, 经过了全世界学家所进行的高品质的验证工作, 而对于自制的密码算法则很难进行这样的验证.
3.9 本章小结
巨大的密钥空间能够抵御暴力破解, 算法上没有弱点可以抵御其他类型的攻击, 这类对称密码就可以通过密文来确保明文的机密性.
为了解决密钥配送问题, 我们需要公钥密码技术. (第 5 章讲解)
尽管使用对称密码可以确保机密性, 但当接收到的密文无法正确解密时, 如果仅仅向发送者返回一个 “出错了” 的消息, 在某些情况下是非常危险的. 因为发送者有可能发送伪造的密文, 并利用解密时返回的错误来盗取信息. (8.5 节详解)
4 分组密码的模式 (分组密码是如何迭代的)
4.2 分组密码的模式
4.2.1 分组密码与流密码
- 分组密码 (block cipher) 是每次只能处理特定长度的一块数据的一类密码算法, 这里的 “一块” 就称为分组 (block). 一个分组的比特数就称为分组长度 (block length).
- 流密码 (stream cipher) 是对数据流进行连续处理的一类密码算法. 流密码中一般以 1 比特, 8 比特或 32 比特等为单位进行加密和解密.
分组密码处理完一个分组就结束了, 不需要通过内部状态来记录加密的进度; 流密码是对一串数据流进行连续处理, 因此需要保持内部状态.
4.2.2 什么是模式
分组密码只能加密固定长度的明文. 如果需要加密任意长度的明文, 就需要对分组密码进行迭代, 而迭代方法就称为分组密码的模式 (mode).
分组密码的主要模式有以下 5 种:
- ECB 模式: Electronic CodeBook mode (电子密码本模式)
- CBC 模式: Cipher Block Chaining mode (密码分组链接模式)
- CFB 模式: Cipher FeedBack mode (密文反馈模式)
- OFB 模式: Output FeedBack mode (输出反馈模式)
- CTR 模式: CounTeR mode (计数器模式)
如果模式选择的不恰当, 明文中的一些规律就可以通过密文被识别出来.
4.2.3 明文分组与密文分组
- 明文分组是指分组密码算法中作为加密对象的明文. 明文分组的长度与分组密码算法的分组长度是相等的.
- 密文分组是指使用分组密码算法将明文分组加密之后所生成的密文.
(明文分组 + 密钥) 用分组密码算法加密 => 密文分组
(密文分组 + 密钥) 用分组密码算法解密 => 明文分组
为了避免 “用分组密码算法加密” 复杂, 本章简写为 “加密”, 省略对密钥的描述.
4.2.4 主动攻击者 Mallory
本章中会出现一个新概念 (主动攻击者 Mallory). 窃听者 Eve 只能被动地进行窃听, 而主动攻击者则可以主动介入发送者和接收者之间的通信过程, 进行阻碍通信或者是篡改密文等活动. 这个名字可能是来自 “恶意的” (malicious) 一词.
4.3 ECB 模式
将明文分组直接加密的方式就是 ECB 模式, 这种模式非常简单, 但由于存在弱点因此通常不会被使用.
4.3.1 什么是 ECB 模式
ECB 模式 的全称是 Electronic CodeBook 模式. 在 ECB 模式中, 将明文分组加密之后的结果将直接成为密文分组.
该模式下相同的明文分组会被转换为相同的密文分组, 可以理解为是一个巨大的 “明文分组 -> 密文分组” 的对应表, 因此 ECB 模式也称为电子密码本模式.
当最后一个明文分组的内容西小于分组长度时, 需要用一些特定的数据进行填充 (padding).
4.3.2 ECB 模式的特点
ECB 模式中, 明文分组与密文分组是一一对应的关系, 如果明文中存在多个相同的明文分组, 则这些明文分组最终都将被转换为相同的密文分组. 因此观察一下密文, 就可以知道明文中存在怎样的重复组合, 并可以以此为线索来破译密码, 因此 ECB 模式是存在一定风险的.
4.3.3 对 ECB 模式的攻击
假设存在主动攻击者, 他能够改变密文分组的顺序. 当接收者对密文进行解密时, 由于分组密码的顺序被改变了, 因此相应的明文分组的顺序也会被改边. 就是说, 攻击者无需破译密码就能够操纵明文. 这个场景中, 攻击者不需要破译密码, 也不需要知道分组的密码算法, 他只要知道哪个分组记录了什么样的数据 (电文的格式) 就可以了.
// 介绍了对调首付款人密文分组的攻击
在 ECB 模式中, 只要对任意密文分组进行替换 (删除/复制), 相应的明文分组也会被替换 (删除/复制).
4.4 CBC 模式
CBC 模式是将前一个密文分组与当前明文分组的内容混合起来进行加密的, 这样就可以避免 ECB 模式的弱点.
4.4.1 什么是 CBC 模式
CBC 模式 的全称是 Cipher Block Chaining 模式 (密文分组链接模式), 因为密文分组是像链条一样相互连接在一起的.
在 CBC 模式中, 首先将明文分组与前一个密文分组进行 XOR 运算, 然后再进行加密.
4.4.2 初始化向量
当加密第一个明文分组时, 由于不存在 “前一个密文分组”, 因此需要事先准备一个长度为一个分组的比特序列来代替 “前一个密文分组”, 这个比特序列称为初始化向量 (Initialization Vector), 通常缩写为 IV. 一般来说每次加密时都会随机产生一个不同的比特序列来作为初始化向量.
4.4.3 CBC 模式的特点
明文分组在加密之前一定会与 “前一个密文分组” 进行 XOR 运算, 因此即便明文分组 1 和 2 的值是相等的, 密文分组 1 和 2 的值也不一定是相等的. 这样 ECB 模式的缺陷在 CBC 模式中就不存在了.
CBC 模式中无法单独对一个中间的明文分组进行加密. 如果要生成密文分组 3, 则至少需要凑齐明文分组 1, 2, 3 才行.
解密时, 假设 CBC 模式加密的密文分组中有一个分组损坏了 (例如由于硬盘故障导致密文分组的值发生了改变等). 只要密文分组的长度没有发生变化, 则解密时最多只会有 2 个分组受到数据损坏的影响.
假设 CBC 模式的密文分组中有一些比特缺失了 (例如由于通信错误导致没有收到某些比特等), 那么此时即便只缺失了 1 比特, 也会导致密文分组的长度发生变化, 此后的分组发生错位, 这样缺失比特的位置之后的密文分组也就全部无法解密了.
4.4.4 对 CBC 模式的攻击
对初始化向量任意比特反转, 第一个明文分组中相应的比特也会被反转.
其中一个密文分组中存在缺失, 之后的所有明文分组都会受到影响.
攻击者可以对初始化向量进行攻击, 但是想要对密文分组也进行同样的攻击 (就是只让明文分组中所期望的比特发生变化) 就非常困难了. 例如对密文分组 1 中的某个比特进行了反转, 则明文分组 1 和明文分组 2 都会受到影响.
通过使用第 8 章中介绍的消息认证码, 还能够判断出数据有没有被篡改.
4.4.5 填充提示攻击
填充提示攻击 (Padding Oracle Attack) 是一种利用分组密码中的填充部分来进行攻击的方法. 在填充提示攻击中, 攻击者会反复发送一段密文, 每次发送时都对填充的数据进行少许改变. 由于接收者 (服务器) 在无法正确解密时会返回一个错误消息, 攻击者通过这一错误消息就可以获得一部分与明文相关的信息. 这一攻击方式适用于所有需要进行分组填充的模式. 2014年对 SSL3.0 造成重大影响的 POODLE 攻击实际上就是一种填充提示攻击. 要预防这种攻击, 需要对密文进行认证, 确保这段密文的确是由合法的发送者在知道明文内容的前提下生成的.
4.4.6 对初始化向量 (IV) 进行攻击
初始化向量 (IV) 必须使用不可预测的随机数. 然而在 SSL/TLS1.0 版本协议中, IV 并没有使用不可预测的随机数, 而是使用了上一次 CBC 模式加密时的最后一个分组. 为了防御攻击者对此进行攻击, TLS1.1 以上的版本中改为了必须显式地传送 IV (RFC5246 6.2.3.2). 关于随机数相关内容, 12章详解.
4.5 CFB 模式
4.5.1 什么是 CFB 模式
CFB 模式 的全程是 Cipher FeedBack 模式 (密文反馈模式). 前一个密文分组会被送回到密码算法的输入端. 反馈指的就是返回输入端的意思.
在 CBC 模式中, 明文分组和密文分组之间有 XOR 和密码算法两个步骤.
而在 CFB 模式中, 明文分组和密文分组之间只有 XOR.
生成第一个密文分组时, 由于不存在前一个输出的数据, 因此需要使用初始化向量 (IV).
4.5.3 CFB 模式与流密码
CFB 模式中, 密码算法的输出相当于一次性密码本中的随机比特序列. 由于密码算法的输出是通过计算得到的, 并不是真正的随机数, 因此 CFB 模式不可能像一次性密码本那样具备理论上不可破译的性质.
CFB 模式中由密码算法所生成的比特序列称为密钥流 (key stream). 在 CFB 模式中, 密码算法就相当于用来生成密钥流的伪随机数生成器, 而初始化向量就相当于伪随机数生成器的 “种子”. 关于伪随机数生成器和种子, 将在 12 章详细讨论.
CFB 模式中, 明文数据可以被逐比特加密, 因此我们可以将 CFB 模式看作是一种 使用分组密码来实现流密码 的方式.
4.5.5 对 CFB 模式的攻击
可以实施重放攻击 (replay attack).
A 向 B 发送了一条由 4 个密文分组组成的消息. 主动攻击者 M 将消息中的后 3 个密文分组保存了下来. 隔天 A 使用相同的密钥向 B 发送了 4 个密文分组, M 用昨天保存的 3 个密文分组将今天发送的后 3 个密文分组进行了替换.
当 B 解密时, 4 个分组中就只有第 1 个可以解密成正确的明文分组, 第 2 个会出错, 而第 3 个和第 4 个则变成了被 M 替换的内容. M 没有破解密码, 就成功地将以前的电文混入了新电文中. 而第 2 个分组出错到底是通信错误呢, 还是被人攻击所造成的呢? B 是无法做出判断的. 要做出这样的判断, 需要使用第 8 章介绍的消息认证码.
4.6 OFB 模式
4.6.1 什么是 OFB 模式
Output-Feedback 模式 (输出反馈模式) 中, 密码算法的输出会反馈到密码算法的输入中.
OFB 模式通过将 “明文分组” 和 “密码算法的输出” 进行 XOR 来产生 “密文分组” 的, 这一点跟 CFB 模式非常相似.
也需要 初始化向量 (IV).
4.6.3 CFB 模式 与 OFB 模式 的对比
区别仅仅在于密码算法的输入.
- CFB: 密文分组被反馈到加密算法的输入
- OFB: 加密算法的输出被反馈到加密算法的输入
CFB 模式中需要对密文分组进行反馈, 因此无法跳过明文分组 1 而先对明文分组 2 进行加密.
OFB 模式中 XOR 所需要的比特序列 (密钥流) 可以事先通过密码算法生成, 和明文分组无关. 意味着生成密钥流的操作和进行 XOR 运算的操作是可以并行的.
4.7 CTR 模式
CounTeR 模式 (计数器模式), 是一种通过将逐次累加的计数器进行加密来生成密钥流的流密码.
CTR 模式中, 每个分组对应一个逐次累加的计数器, 并通过对计数器进行加密来生成密钥流.
4.7.1 计数器的生成方法
每次加密时都会生成一个不同的值 (nonce) 来作为计数器的初始值.
计数器的初始值可能是像 nonce 拼接 分组序号 的形式.
这种形式可以保证计数器的值每次都不同.
4.7.2 OFB 模式 与 CTR 模式的对比
CTR 模式 和 OFB 模式 一样都属于流密码.
- OFB: 将加密的输出反馈到输入
- CTR: 将计数器的值用作输入
4.7.3 CTR 模式的特点
CTR 模式中可以以任意顺序对分组进行加密和解密, 因为加密和解密时需要用到的 “计数器” 的值可以由 nonce 和 分组序号 直接计算出来, 这一性质是 OFB 模式所不具备的. 在支持并行计算的系统中 CTR 模式的速度是非常快的.
4.7.4 错误与机密性
错误与机密性方面, CTR 模式也具备和 OFB 模式差不多的性质.
假设 CTR 模式的密文分组中有一个比特被反转了, 则解密后明文分组中仅有与之对应的比特会被反转, 这一错误不会放大.
换言之, CTR 模式中, 主动攻击者 M 可以通过反转密文分组中的某些比特, 引起解密后明文中的相应比特也发生反转, 这一弱点和 OFB 模式是相同的.
在 OFB 模式中, 如果对密钥流的一个分组进行加密后其结果碰巧和加密前是相同的, 那么这一分组之后的密钥流就会变成同一值的不断反复. 在 CTR 模式中就不存在这一问题.
专栏: GCM 模式
在 CTR 模式的基础上增加 “认证” 功能的模式称为 GCM 模式 (Galois/Counter Mode). 这一模式能够在 CTR 模式生成密文的同时生成用于认证的信息, 从而判断 “密文分组是否通过合法的加密过程生成”. 这一机制能够识别出 “这段密文是伪造的”. 第 8 章中详解.
4.8 应该使用哪种模式呢
作者在书中附上了模式比较表, 参考了 应用密码学 [Schneier, 1996]一书中的内容.
实用密码学 (Practical Cryptography) [Schneier, 2003] 一书中推荐使用 CBC 模式 和 CTR 模式, 而 CRYPTREC 密码清单 中推荐使用 CBC, CFB, OFB 和 CTR 模式.
5 公钥密码 (用公钥加密, 用私钥解密)
5.3 密钥配送问题
现实世界中使用对称密码时, 一定会遇到 密钥配送问题 (key distribution problem). 有以下几种解决方法:
- 通过事先共享密钥来解决
- 通过密钥分配中心来解决
- 通过 Diffie-Hellman 密钥交换来解决
- 通过公钥密码来解决
5.4 公钥密码
5.4.1 什么是公钥密码
公钥密码 (public-key cryptography) 中, 密钥分为 加密密钥 和 解密密钥 两种:
- 加密密钥: 一般是公开的, 因此该密钥被称为 公钥 (public key).
- 解密密钥: 绝对不能公开的, 这个密钥只能由你自己来使用, 因此称为 私钥 (private key).
公钥和私钥是一一对应的, 一对公钥和私钥统称为密钥对 (key pair).
5.4.4 各种术语
非对称密码 (asymmetric cryptography) 和 公钥密码 表示同一个含义, 这一术语是相对于对称密码而言的.
私钥 (private key) 也有很多同义的别名, 例如个人密钥, 私有密钥, 非公开密钥等. 也有人将其称为 秘密密钥 (secret key), 不过这个词也可以指对称密码的密钥, 因此在使用时需要注意. 出于这个原因, 也有人将对称密码的密钥称为共享密码密钥, 将公钥密码的私钥称为私有秘密密钥以示区别.
5.4.5 公钥密码无法解决的问题
公钥密码解决了密钥配送问题, 并不意味着它能够解决所有的问题. 我们需要判断得到的公钥是否正确合法, 这个问题被称为 公钥认证 问题. 后续章讲解.
公钥密码的处理速度只有对称密码的几百分之一, 下一章介绍.
5.5 时钟运算
// 这一节主要给后面讲 RSA 做数学方面的铺垫.
5.6 RSA
5.6.1 什么是 RSA
RSA 是一种公钥密码算法, 它的名字是由它的三位开发者, 即 Ron Rivest, Adi Shamir 和 Leonard Adleman 的姓氏的首字母组成的 (Rivest-Shamir-Adleman).
RSA 可以被用于公钥密码和数字签名, 第 9 章节讲解数字签名.
1983 年, RSA 公司为 RSA 算法在美国取得了专利, 但现在该专利已经过期.
5.6.- RSA 加密, 解密, 生成密钥对, 具体实践
// 还是看书吧
5.7 对 RSA 的攻击
5.7.1 通过密文来求得明文
通过 RSA 加解密过程可以得知, 通过密文求明文相当于求离散对数的问题, 这是非常困难的, 因为人类还没有发现求离散对数的高效算法.
5.7.2 通过暴力破解来找出 D
暴力破解的难度会随着 D 的长度增大而变大, 当 D 足够长时, 就不可能在现实的时间内通过暴力破解找出数 D.
5.7.3 通过 E 和 N 求出 D
质数 p 和 q 不能被密码破译者知道.
- 对 N 进行质因数分解攻击
求 p 和 q 只能通过将 N 进行质因数分解, 一旦发现了对大整数进行质因数分解的高效算法, RSA 就能够被破译. - 通过推测 p 和 q 进行攻击
由于 p 和 q 是通过伪随机数生成器产生的, 如果伪随机数生成器的算法很差, 密码破译者就有可能推测出来 p 和 q, 使用能够被推测出来的随机数是非常危险的. - 其他攻击
只要对 N 进行质因数分解并求出 p 和 q, 就能够求出 D.
但是至于 “求 D” 与 “对 N 进行质因数分解” 是否是等价的, 这个问题需要通过数学方法证明. 2004 年 Alexander May 证明了 “求 D” 与 “对 N 进行质因数分解” 在确定性多项式时间内是等价的.
这样的方法目前还没有出现, 而且我们也不知道是否真的存在这样的方法.
5.7.4 中间人攻击
中间人攻击 (man-in-the-middle attack) 虽然不能破译 RSA, 但却是一种针对机密性的有效攻击. 这种攻击可以针对任何公钥密码.
要防御中间人攻击, 还需要一种手段来确认所收到的公钥是否真的属于 B, 这种手段称为认证. 这种情况下我们可以使用公钥的证书. 第 10 章探讨.
5.7.5 选择密文攻击
选择密文攻击 (Chosen Ciphertext Attack) 中, 假设攻击者可以使用这样一种服务, 即 “发送任意数据, 服务器都会将其当作密文来解密并返回解密的结果”, 这种服务被称为 解密提示 (Decryption Oracle). 上面提到的 “任意数据” 并不包括攻击者试图攻击的那一段密文本身. 能够利用解密提示, 对于攻击者来说是一个非常有利的条件. 因为他可以生成各种不同的数据, 并让解密提示来尝试解密, 从而获得与生成想要攻击的密文时使用的密钥以及明文有关的部分信息. 反过来说, 如果一种密码算法能够抵御选择密文攻击, 则我们就可以认为这种算法的强度很高.
只要我们在解密时能够判断 “密文是否是由知道明文的人通过合法的方式生成的” 就可以了. RSA-OAEP (Optimal Asymmetric Encryption Padding, 最优非对称加密填充) 正是基于上述思路设计的一种 RSA 改良算法 (RFC2437).
RSA-OAEP 在加密时会在明文前面填充一些认证信息, 包括明文的散列值以及一定数量的 0, 然后再对填充后的明文用 RSA 进行加密. 在 RSA-OAEP 的解密过程中, 如果在 RSA 解密后的数据的开头没有找到正确的认证信息, 则可以断定 “这段密文不是由知道明文的人生成的”, 并返回一条固定的错误信息 “decryption error” (这里的重点是, 不能将具体的错误内容告知发送者). 这样一来, 攻击者就无法通过 RSA-OAEP 的解密提示获得有用的信息, 因此这一算法能够抵御选择密文攻击. 在实际运用中, 还会通过随机数使得每次生成的密文呈现不同的排列方式, 进而进一步提高安全性.
5.8 其他公钥密码
5.8.1 ElGamal 方式
ElGamal 方式利用了 modN 下求离散对数的困难度. 有一个缺点是加密的密文长度会变为明文的两倍. 密码软件 GnuPG 中就支持这种方式.
5.8.2 Rabin 方式
Rabin 方式利用了 mod N 下求平方根的困难度.
5.8.3 椭圆曲线密码
椭圆曲线密码 (Elliptic Curve Cryptography, ECC) 是最近备受关注的一种公钥密码算法. 它的特点是所需的密钥长度比 RSA 短. 它是通过将椭圆曲线上的特定点进行特殊的乘法运算来实现的, 它利用了这种乘法运算的逆运算非常困难这一特性.
5.9 关于公钥密码的 Q&A
公钥密码比对称密码的机密性更高吗?
这个问题无法回答, 因为机密性的高低是根据密钥长度而变化的.密钥长度为 256 比特的对称密码 AES, 与密钥长度为 1024 比特的公钥密码 RSA 相比, RSA 的安全性更高吗?
不是. 公钥密码的密钥长度不能直接与对称密码的密钥长度进行比较, 而且对不同密码算法的强度进行比较本来就不是一件容易的事.
尽管如此, 在将对称密码和公钥密码结合起来使用的场景中, 我们还是希望使两者的强度保持一定的平衡. 很多密码系统中都会给出一些密码算法的理想组合方式, 并打包成密码套件 (cipher suite).
在强度相对均衡的前提下, AES 的密钥长度和 RSA 的密钥长度可以参照基于 NIST 的密码强度比较表 (NIST Special Publication 800-57, Recommendation for Key Management). 通过表可以看出, 密钥长度为 256 比特的 AES, 与密钥长度为 15360 比特的 RSA 具备均衡的强度.因为已经有了公钥密码, 今后对称密码会消失吗?
不会. 一般来说, 采用具备同等机密性的密钥长度的情况下, 公钥密码的处理速度只有对称密码的几百分之一. 因此, 公钥密码并不适合用来对很长的消息内容进行加密. 根据目的的不同, 还可能会配合使用对称密码和公钥密码, 例如第 6 章介绍的混合密码系统.随着越来越多的人在不断地生成 RSA 密钥对, 质数会不会被用光呢?
不需担心. 512 比特能够容纳的质数的数量大约为 10 的 150 次方, 这个数量比宇宙中原子的数量还多. 别人生成的质数组合和自己生成的质数组合偶然撞车的可能性, 事实上也可以认为是没有的.RSA 加密过程中, 需要对大整数进行质因数分解吗?
不需要. RSA 在加密, 解密, 密钥对生成的过程中都不需要对大整数进行质因数分解. 只有在需要由数 N 求 p 和 q 的密码破译过程中才需要对大整数进行质因数分解, 因此 RSA 的设计是将质因数分解这种困难的问题留给了密码破译者.RSA 的破译与大整数的质因数分解是等价的吗?
2004 年 Alexander May 证明了求 RSA 的私钥和对 N 进行质因数分解是等价的.要抵御质因数分解, N 的长度需要达到多少比特呢?
N 无论有多长, 总有一天能够被质因数分解, 因此现在的问题是, 在现实的时间内 N 是否能够被质因数分解. 随着计算机性能的提高, 对一定长度的整数进行质因数分解所需要的时间会逐步缩短, 如果大型组织或者国家投入其计算资源, 则时间还会进一步缩短.
随着计算机技术的进步等, 以前被认为是安全的密码会被破译, 这一现象称为密码劣化. 针对这一点, NIST SP800-57 中给出了如下方针:
- 1024 比特的 RSA 不应被用于新的用途
- 2048 比特的 RSA 可在 2030 年之前被用于新的用途
- 4096 比特的 RSA 在 2031 年之后仍可被用于新的用途
6 混合密码系统 (用对称密钥提高速度, 用公钥密码保护会话密钥)
混合密码系统 (hybrid cryptosystem) 用对称密码来加密明文, 用公钥密码来加密对称密码中所使用的密钥. 它能够在通信中将对称密码和公钥密码的优势结合起来.
第 2 部分 认证
7 单向散列函数 (获取消息的 “指纹”)
7.2.2 什么是单向散列函数
单向散列函数 (one-way hash function) 有一个输入和一个输出, 其中输入称为 消息 (message), 输出称为 散列值 (hash value).
7.2.3 单向散列函数的性质
根据任意长度的消息计算出固定长度的散列值
能够快速计算出散列值
消息不同散列值也不同
两个不同消息产生同一个散列值的情况称为碰撞 (collision). 难以发现碰撞的特性称为抗碰撞性 (collision resistance). 单向散列函数必须确保要找到和该条消息具有相同散列值的另外一条消息是非常困难的. 这一特性称为弱抗碰撞性. 相对的, 还有强抗碰撞性, 是指要找到散列值相同的两条不同的消息是非常困难的这一性质. 密码技术中所使用的单向散列函数, 不仅要具备弱抗碰撞性, 还必须具备强抗碰撞性.具备单向性
根据消息计算出散列值很容易, 但根据散列值无法反算出消息. 单向散列函数并不是一种加密, 无法通过解密将散列值还原为原来的消息.
7.2.4 关于术语
单向散列函数也称为消息摘要函数 (message digest function), 哈希函数或者杂凑函数.
输入单向散列函数的消息也称为原像 (pre-image).
单向散列函数输出的散列值也称为消息摘要 (message digest) 或者指纹 (fingerprint).
完整性也称为一致性.
7.3 单向散列函数的实际应用
7.3.1 检测软件是否被篡改
用户通过多种途径 (镜像站点) 下载到软件之后, 可以自行计算散列值, 然后与官方网站上公布的散列值进行对比, 可以确认自己所下载到的文件与软件作者所提供的文件是否一致.
7.3.2 基于口令的加密
单向散列函数也被用于基于口令的加密 (Password Based Encryption, PBE).
PBE 的原理是将口令和盐 (salt, 通过伪随机数生成器产生的随机值) 混合后计算其散列值, 然后将这个散列值用作加密的密钥. 通过这样的方法能够预防针对口令的字典攻击. 11 章详解.
7.3.3 消息认证码
消息认证码是将 “发送者和接收者之间的共享密钥” 和 “消息” 进行混合后计算出的散列值. 可以检测并防止通信过程中的错误, 篡改以及伪装.
消息认证码在 SSL/TLS 中也得到了运用, SSL/TLS 在 14 章介绍.
7.3.4 数字签名
数字签名的过程非常耗时, 因此一般不会对整个消息内容直接施加数字签名, 而是通过单向散列函数计算出消息的散列值, 然后再对这个散列值施加数字签名. 第 9 章介绍.
7.3.5 伪随机数生成器
密码技术中所使用的随机数需要具备 “事实上不可能根据过去的随机数列预测未来的随机数列” 这样的性质. 为了保证不可预测性, 可以利用单向散列函数的单向性. 第 12 章介绍.
7.3.6 一次性口令
使用单向散列函数可以构造 一次性口令 (one-time password). 一次性口令经常被用于服务器对客户端的合法认证. 在这种方式中, 通过使用单向散列函数可以保证口令只在通信链路上传送一次, 因此即使窃听者窃取了口令, 也无法使用.
7.4 单向散列函数的具体例子
7.4.1 MD4, MD5
随着 Dobbertin 提出寻找 MD4 散列碰撞的方法, 现在它已经不安全了.
MD5 的强抗碰撞性已经被攻破, 现在已经能够产生具备相同散列值的两条不同的消息, 因此它也已经不安全了.
MD4 和 MD5 中的 MD 是消息摘要 (Message Digest) 的缩写.
7.4.2 SHA-1, SHA-256, SHA-384, SHA-512
在 CRYPTREC 密码清单 中, SHA-1 已经被列入 “可谨慎运用的密码清单”, 即除了用于保持兼容性的目的以外, 其他情况下都不推荐使用.
SHA-256, SHA-384, SHA512 都是由 NIST (National Institute of Standards and Technology) 设计的单向散列函数, 它的散列值长度分别为 256 比特, 384 比特, 512 比特. 这些单向散列函数合起来统称 SHA-2.
SHA-1 的强抗碰撞性已于 2005 年被攻破, 现在已经能够产生具备相同散列值的两条不同的消息. 不过, SHA-2 还尚未被攻破.
7.4.3 RIPEMD-160
在 CRYPTREC 密码清单 中, RIPEMD-160 已经被列入 “可谨慎运用的密码清单”, 即除了用于保持兼容性的目的以外, 其他情况下都不推荐使用.
RIPEMD 的强抗碰撞性已经于 2004 年被攻破, 但 RIPEMD-160 还尚未被攻破. 比特币中使用的就是 RIPEMD-160.
7.4.4 SHA-3
SHA-3 和 AES 一样采用公开竞争的方式进行标准化. SHA-3 的选拔于 2012 年尘埃落定, 一个名叫 Keccak 的算法胜出, 最终成为了 SHA-3.
7.6 Keccak
Keccak 可以生成任意长度的散列值, 但为了配合 SHA-2 的散列值长度, SHA-3 标准中共规定了 SHA3-224, SHA3-256, SHA3-384, SHA3-512 这 4 种版本. SHA-3 没有输入数据的长度限制.
7.6.3 双工结构
双工结构作为海绵结构的变形, 它的输入和输出是以相同的速率进行的. 在双向通信中, 发送和接收同时进行的方式称为全双工 (full duplex), Keccak 的双工结构也代表同样的含义.
采用双工结构, Keccak 不仅可以用于计算散列值, 还可以覆盖密码学家的工具箱中的其他多种用途, 如伪随机数生成器, 流密码, 认证加密, 消息认证码等.
7.6.4 Keccak 的内部状态
由于内部状态可以代表整个处理过程中的全部中间状态, 因此有利于节约内存. Keccak 用到了很多比特单位的运算, 因此被认为可以有效抵御针对字节单位的攻击.
7.6.6 对 Keccak 的攻击
Keccak 之前的单向散列函数都是通过循环执行压缩函数的方式来生成散列值的, 这种方式称为 MD 结构 (Merkle-Damgard construction). MD4, MD5, RIPEMD, RIPEMD-160, SHA-1, SHA-2 等几乎所有的传统单向散列函数算法都是基于 MD 结构的.
Keccak 采用了和 MD 结构完全不同的海绵结构, 因此针对 SHA-1 的攻击方法对 Keccak 是无效的.
到目前为止, 还没有出现能够对实际运用中的 Keccak 算法形成威胁的攻击方法.
7.6.7 对缩水版 Keccak 的攻击竞赛
因为我们可以比较容易地分析缩水版的 Keccak, 也就能够比较容易地对实际运用的标准版算法的强度进行评估, 而作为一个将在全世界广泛使用的单向散列函数算法, “易于分析” 可以说是一个十分优秀的特性.
7.7 应该使用哪种单向散列函数呢
MD5 是不安全的, 因此不应该使用.
SHA-1 除了用于对过去生成的散列值进行校验之外, 不应该被用于新的用途, 而是应该迁移到 SHA-2.
SHA-2 有效应对了针对 SHA-1 的攻击方法, 因此是安全的, 可以使用.
SHA-3 是安全的, 可以使用.
2013 年发布的 CRYPTREC 密码清单 中, SHA-2 (SHA-256, SHA-384, SHA-512) 被列入了 “电子政府推荐使用的密码清单” 中.
和对称密码算法一样, 我们不应该使用任何自制算法.
7.8 对单向散列函数的攻击
7.8.1 暴力破解 (攻击故事1)
任何文件中都或多或少地具有一定的冗余性, 利用文件的冗余性生成具有相同散列值的另一个文件, 这就是一种针对单向散列函数的攻击.
正如对密码可以进行暴力破解一样, 对单向散列函数也可以进行暴力破解.
需要寻求的是一条具备特定散列值的消息, 这相当于一种试图破解单向散列函数的 “弱抗碰撞性” 的攻击. 这种情况下, 暴力破解需要尝试的次数可以根据散列值的长度计算出来. 以 SHA3-512 为例, 由于它的散列值长度为 512 比特, 因此最多只要尝试 2^512 次就能够找到目标消息了, 如此多的尝试次数在现实中是不可能完成的.
找出具有指定散列值的消息的攻击分为两种, 即 “原像攻击” 和 “第二原像攻击”. 原像攻击 (Pre-Image Attack) 是指给定一个散列值, 找出具有该散列值的任意消息; 第二原像攻击 (Second Pre-Image Attack) 是指给定一条消息 1, 找出另外一条消息 2, 消息 2 的散列值和消息 1 相同.
7.8.2 生日攻击 (攻击故事2)
M 准备了两份具有相同散列值的合同交给 A 让她计算散列值, 随后将两个合同掉包. 在这里 M 不是寻找生成特定散列值的消息, 而是要找到散列值相同的两条消息, 而散列值则可以是任意值. 这样的攻击, 一般称为 生日攻击 (birthday attack) 或者 冲突攻击 (collision attack), 这是一种*试图破解单向散列函数的 “强抗碰撞性” 的攻击.
生日攻击的原理就是来自生日悖论, 也就是利用了 “任意散列值一致的概率比想象中要高” 这样的特性.
以 512 比特的散列值为例, 对单向散列函数进行暴力破解所需要的尝试次数为 2^512 次, 而对同一单向散列函数进行生日攻击所需的尝试次数为 2^256 次, 因此和暴力破解相比, 生日攻击所需的尝试次数要少得多.
7.9 单向散列函数无法解决的问题
假设主动攻击者 M 伪装成 A, 向 B 同时发送了消息和散列值. 这时 B 能够通过单向散列函数检查消息的完整性, 但是这只是对 M 发送的消息进行检查, 而无法查出发送者的身份是否被 M 进行了伪装. 也就是说, 单向散列函数能够辨别出 “篡改”, 但无法辨别出 “伪装”.
仅靠完整性检查是不够的, 我们还需要进行认证.
用于认证的技术包括消息验证码和数字签名. 消息认证码能够向通信对象保证消息没有被篡改, 而数字签名不仅能够向通信对象保证消息没有被篡改, 还能够向所有第三方做出这样的保证.
7.11 小测验的答案
鸽巢原理 (pigeon-hole principle). 这个名字来自 “将 N + 1 只鸽子分别装到 N 个鸽巢中时, 必然至少有一个鸽巢中存在两只或两只以上的鸽子” 这一 (理所当然) 事实.
8 消息认证码 (消息被正确传送了吗)
8.2.2 什么是消息认证码
消息认证码 (Message Authentication Code) 是一种确认完整性并进行认证的技术, 取三个单词的首字母, 简称为 MAC.
消息认证码的输入包括任意长度的消息和一个发送与接收者之间共享的密钥, 它可以输出固定长度的数据, 这个数据称为MAC值.
消息认证码有很多种实现方式, 可以暂且这样理解: 消息认证码是一种与密钥相关联的单向散列函数.
对称密码的密钥配送问题在消息认证码中也同样会发生.
8.3 消息认证码的应用实例
8.3.1 SWIFT
SWIFT 的全称是 Society for Worldwide Interbank Financial Telecommunication (环球银行金融电信协会), 是于 1973 年成立的一个组织, 其目的是为国际银行间的交易保驾护航.
银行和银行之间是通过 SWIFT 来传递交易消息的. 而为了确认消息的完整性以及对消息进行验证, SWIFT 中使用了消息认证码.
在使用公钥密码进行密钥交换之前, 消息认证码所使用的共享密钥都是由人来进行配送的.
8.3.2 IPsec
IPsec 是对互联网基本通信协议 IP 协议 (Internet Protocol) 增加安全性的一种方式. 在 IPsec 中, 对通信内容的认证和完整性校验都是采用消息认证码来完成的.
8.3.3 SSL/TLS
SSL/TLS 是我们在网上购物等场景中所使用的通信协议. SSL/TLS 中对通信内容的认证和完整性校验也使用了消息认证码.
8.4 消息认证码的实现方法
8.4.1 使用单向散列函数实现
使用 SHA-2 之类的单向散列函数可以实现消息认证码, 其中一种实现方法称为HMAC.
8.4.2 使用分组密码实现
使用 AES 之类的分组密码可以实现消息认证码.
将分组密码的密钥作为消息认证码的共享密钥来使用, 并用 CBC 模式将消息全部加密. 此时, 初始化向量 (IV) 是固定的. 由于消息认证码中不需要解密, 因此将除最后一个分组以外的密文部分全部丢弃, 而将最后一个分组用作 MAC 值. 由于 CBC 模式的最后一个分组会受到整个消息以及密钥的双重影响, 因此可以将它用作消息认证码. 例如, AES-CMAC (RFC4493) 就是一种基于 AES 来实现的消息认证码.
8.4.3 其他实现方法
使用流密码和公钥密码等也可以实现消息认证码.
8.5 认证加密
2000 年以后, 关于认证加密 (缩写为 AE (Authenticated Encryption) 或 AEAD (Authenticated Encryption with Associated Data)) 的研究逐步展开. 认证加密是一种将对称密码与消息认证码相结合, 同时满足机密性, 完整性和认证三大功能的机制.
有一种认证加密方式叫做 Encrypt-then-MAC, 这种方式是先用对称密码将明文加密, 然后计算密文的 MAC 值. 通过 MAC 值就可以判断 “这段密文的确是由知道明文和密钥的人生成的”. 使用这一机制, 可以防止攻击者 M 通过发送任意伪造的密文, 并让服务器解密来套取信息的攻击 (选择密文攻击, 参见 5.7.5 节).
除了 Encrypt-then-MAC 之外, 还有其他一些认证加密方式, 如 Encrypt-and-MAC (将明文用对称密码加密, 并对明文计算 MAC 值) 和 MAC-then-Encrypt (先计算明文的 MAC 值, 然后将明文和 MAC 值同时用对称密码加密).
- GCM 与 GMAC
GCM (Galois/Counter Mode) 是一种认证加密方式. GCM 中使用 AES 等 128 比特分组密码的 CTR 模式 (参见 4.7 节), 并使用一个反复进行加法和乘法运算的散列函数来计算 MAC 值. 由于 CTR 模式的本质是对递增的计数器值进行加密, 因此可通过对若干分组进行并行处理来提高运行速度. 此外, 由于 CTR 模式加密与 MAC 值的计算使用的是相同的密钥, 因此在密钥管理方面也更加容易. 专门用于消息认证码的 GCM 称为 GMAC. 在 CRYPTREC 密码清单 中, GCM 和 CCM (CBC Counter Mode) 都被列为了推荐使用的认证加密方式.
8.6 HMAC 的详细介绍
8.6.1 什么是 HMAC
HMAC 是一种使用单向散列函数来构造消息认证码的方法 (RFC2104), 其中 HMAC 的 H 就是 Hash 的意思.
HMAC 中所使用的单向散列函数并不仅限于一种, 任何高强度的单向散列函数都可以被用于 HMAC, 如果将来设计出新的单向散列函数, 也同样可以使用.
使用 SHA-1, SHA-224, SHA-256, SHA-384, SHA-512 所构造的 HMAC, 分别称为 HMAC-SHA11, HMAC-SHA-224, HMAC-SHA-256, HMAC-SHA-384, HMAC-SHA-512.
8.6.2 HMAC 的步骤
// 看书
通过步骤流程可以看出, 最后得到的 MAC 值, 一定是一个和输入的消息以及密钥都相关的长度固定的比特序列.
8.7 对消息认证码的攻击
8.7.1 重放攻击
例子里 M 没有破解消息认证码, 而只是将 A 的正确 MAC 值保存下来重复利用而已. 这种攻击方式称为重放攻击 (replay attack).
有几种方法可以预防重放攻击:
- 序号
约定每次都对发送的消息赋予一个递增的编号 (序号), 并且在计算 MAC 值时将序号也包含在消息中. 由于 M 无法计算序号递增之后的 MAC 值, 因此就可以防御重放攻击. 这种方法虽然有效, 但是对每个通信对象都需要记录最后一个消息的序号. - 时间戳
约定在发送消息时包含当前的时间, 如果收到以前的消息, 即便 MAC 值正确也将其当做错误的消息来处理, 这一就能够防御重放攻击. 这种方法虽然有效, 但是发送者和接收者的时钟必须一致, 而且考虑到通信的延迟, 必须在时间的判断上留下缓冲, 于是多多少少还是会存在可以进行重放攻击的时间. - nonce
在通信之前, 接收者先向发送者发送一个一次性的随机数, 这个随机数一般称为 nonce. 发送者在消息中包含这个 nonce 并计算 MAC 值. 由于每次通信时 nonce 的值都会发生变化, 因此无法进行重放攻击. 这种方法虽然有效, 但通信的数据量会有所增加.
8.7.2 密钥推测攻击
和对单向散列函数的攻击一样, 对消息认证码也可以进行暴力破解 (7.8.1 节) 以及生日攻击 (7.8.2 节).
对于消息认证码来说, 应保证不能根据 MAC 值推测出通信双方所使用的密钥.
8.8 消息认证码无法解决的问题
8.8.1 对第三方证明
假设 B 收到了来自 A 的消息之后, 想要向第三方验证者 V 证明这条消息的确是 A 发送的, 但是用消息认证码无法进行这样的证明.
首先 V 要校验 MAC 值, 就需要知道 A 和 B 之间共享的密钥.
就算 V 拿到共享密钥, 校验过 MAC 值是正确的, V 也无法判断这条消息是由 A 发送的, 可能是持有密钥的 B.
第 9 章中将要介绍的数字签名就可以实现对第三方的证明.
8.8.2 防止否认
上面讲过, B 无法向验证者 V 证明消息来自 A, 也就是说, 发送者 A 可以向 V 声称: “我没有向 B 发送过这条消息.” 这样的行为就称为否认 (repudiation).
A 可以说 “这条消息是 B 自己编的吧” “说不定 B 的密钥被主动攻击者 M 给盗取了, 我的密钥可是妥善保管着呢” 等.
即便 B 拿 MAC 值来举证, V 也无法判断 A 和 B 谁的主张才是正确的, 也就是说, 用消息认证码无法防止否认 (nonrepudiation).
9 数字签名 (消息到底是谁写的)
9.3.2 从消息认证码到数字签名
假设发送者 A 和接收者 B 各自使用不同的密钥. A 发送消息时, 用私钥生成一个 “签名”. 接收者 B 则使用和 A 不同的密钥对签名进行认证. B 的密钥无法根据消息生成签名, 但是用 B 的密钥却可以对 A 所计算的签名进行验证, 也就是说可以知道这个签名是否是通过 A 的密钥计算出来的. 这种看似很神奇的技术早就已经问世了, 这就是数字签名 (digital signature).
- 专栏: 不要和邮件末尾的签名搞混
我们经常会在邮件的末尾附上一段文字来表明自己的名字和所在的公司等信息, 这些文字也称为 “签名”. 邮件的签名和本章所说的数字签名 (签名) 是完全不同的两码事. 在邮件末尾添加的签名是一串固定的文字, 而本章所说的数字签名 (签名) 则是根据消息内容生成的一串 “只有自己才能计算出来的数值”, 因此数字签名 (签名) 的内容是随消息的改变而改变的.
9.3.3 签名的生成和验证
数字签名对签名密钥和验证密钥进行了区分, 使用验证密钥是无法生成签名的. 签名密钥只能由签名的人持有, 而验证密钥则是任何需要验证签名的人都可以持有.
听着似曾相识? 没错, 这就是第 5 章中讲过的公钥密码嘛. 公钥密码和上面讲的数字签名的结构非常相似. 在公钥密码中, 密钥分为加密密钥和解密密钥, 用加密密钥无法进行解密. 此外, 解密密钥只能由需要解密的人持有, 而加密密钥则是任何需要加密的人都可以持有. 你看, 数字签名和公钥密码是不是很像呢?
实际上, 数字签名和公钥密码有着非常紧密的联系, 简而言之, 数字签名就是通过将公钥密码 “反过来用” 实现的.
9.3.4 公钥密码与数字签名
数字签名中同样会使用公钥和私钥组成的密钥对, 不过这两个密钥的用法和公钥密码是相反的, 即用私钥加密相当于生成签名, 而用公钥解密则相当于验证签名.
严格来说, RSA 算法中公钥加密和数字签名正好是完全相反的关系, 但在其他算法中有可能不是这样完全相反的关系.
9.4 数字签名的方法
- 直接对消息签名 (实际上并不会使用)
- 对消息的散列值签名 (实际中一般都使用这种方法)
9.5 对数字签名的疑问
- 密文为什么能够具备签名的意义呢?
数字签名是利用了 “没有私钥的人事实上无法生成使用该私钥所生成的密文” 这一性质来实现的. 这里所生成的密文并非用于保证机密性, 而是被用于代表一种只有持有该密钥的人才能够生成的信息. 这样的信息一般称为认证符号 (authenticator), 消息认证码也是认证符号的一种, 数字签名也是一样. 数字签名是通过使用私钥进行加密来产生认证符号的. - 例子中消息没有经过加密就发送了, 这样不就无法保证消息的机密性了吗?
的确如此, 数字签名的作用本来就不是保证机密性. 如果需要保证机密性, 则可以不直接发送消息, 而是将消息进行加密之后再发送. 关于密码和签名的组合方法, 第 13 章介绍. - 数字签名只是计算机上的一种数据, 很容易被复制, 但如果可以轻易复制出相同的内容, 那还能用作签名吗?
的确, 虽然叫做签名, 但它也仅仅是计算机上的一种普通的数据而已.
但是, 签名可以被复制, 不意味着签名就没有意义, 因为签名所表达的意义是特定的签名者对特定的消息进行了签名, 即便签名被复制, 也并不会改变签名者和消息的内容.
签名是不是被复制的并不重要, 真正重要的是特定的签名者与特定的消息绑定在了一起这一事实. - 数字签名只不过是普通的数据, 消息和签名两者都可以任意修改的, 这样的签名还有意义吗?
的确, 签名之后也可以对消息和签名进行修改, 但是这样修改之后, 验证签名就会失败, 进行验证的人就能够发现这一修改行为. 数字签名所要实现的并不是防止修改, 而是识别修改. - 追问: 能不能同时修改消息和签名, 使得验证签名能够成功呢?
事实上是做不到的. 以对散列值签名为例, 只要消息被修改 1 比特, 重新计算的散列值就会发生很大的变化, 要拼凑出合法的签名, 必须在不知道私钥的前提下对新产生的散列值进行加密, 事实上这是无法做到的, 因为不知道私钥就无法生成用该私钥才能生成的密文. - 如果得到了某人的数字签名, 应该就可以把签名的部分提取出来附加在别的消息后面, 这样的签名还有效吗?
的确, 可以将签名部分提取出来并附加到别的消息后面, 但是验证签名会失效. 在数字签名中, 签名和消息之间是具有对应关系的, 消息不同签名内容也不同, 因此事实上是无法做到将签名提取出来重复使用的. - 如果是纸质的借据, 只要原件撕毁就可以作废. 但是带有数字签名的借据只是计算机文件, 将其删除也无法保证确实已经作废, 因为不知道其他地方是否还留有副本. 无法作废的签名是不是非常不方便呢?
的确, 带有数字签名的借据即便删除掉也无法作废, 要作废带有数字签名的借据, 可以重新创建一份相当于收据的文书, 并让对方在这份文书上加数字签名. 拿一个具体的例子来说, 如果我们想将过去使用过的公钥作废, 就可以创建一份声明该公钥已作废的文书并另外加上数字签名. 也可以在消息中声明该消息的有效期并加上数字签名, 例如公钥的证书就属于这种情况, 第 10 章介绍. - 消息认证码无法防止否认, 为什么数字签名就能够防止否认呢?
防止否认与 “谁持有密钥” 这一问题密切相关. 在消息认证码中, 能够计算 MAC 值的密钥是由发送者和接收者双方共同持有的, 因此任何一方都能够计算 MAC 值. 相对地, 数字签名中, 能够生成签名的密钥 (私钥) 是只有发送者才持有的. 当然, 严格来说, 如果数字签名的生成者说 “我的私钥被别人窃取了”, 也是有可能进行否认的. 第 10 章介绍. - 纸质借据上如果不签名盖章的话, 总是觉得不大放心. 数字签名真的能够有效代替现实世界中的签名和盖章吗?
这个疑问应该说非常合理.
数字签名技术有很多优点, 例如不需要物理交换文书就能够签订合同, 以及可以对计算机上的任意数据进行签名等. 然而, 对于实际上能不能代替签名这个问题还是有一些不安的因素. 其中一个很大的原因恐怕是签订合同, 进行认证这样的行为是一种社会性的行为.
我们在对文件进行数字签名时, 没有人会自己亲手去实际计算数字签名的算法, 而只是在阅读软件给出的提示信息后按下按钮或者输入口令.
然而, 这个软件真的值得信任吗? 软件虽然会提示用户说 “请对该文件签名”, 但软件所提示的消息真的是经过这个软件本身进行的签名吗? 有没有可能是这个软件本身感染了病毒, 而病毒实际上对另外一份文件进行了签名呢? 这样的危险我们还能够想到很多, 而实际上它们确实有可能发生.
美国于 2000 年颁布了 E-SIGN 法案, 日本也于 2001 年颁布了电子签名及其认证业务的相关法律 (电子签名法). 这些法律为将电子手段实现的签名与手写的签名和盖章同等处理提供了法律基础. 然而在实际应用中, 很有可能会产生与数字签名相关的问题以及围绕数字签名有效性的诉讼.
数字签名技术在未来将发挥重要的作用, 但是单纯认为数字签名比普通的印章或手写签名更可信是很危险的. 一种新技术只有被人们广泛地认知, 并对各种问题制定相应的解决办法之后, 才能被社会真正地接受.
10 证书 (为公钥加上数字签名)
第 3 部分 密钥, 随机数与应用技术
11 密钥 (秘密的精华)
12 随机数 (不可预测性的源泉)
12.4.1 对随机数的性质进行分类
这里我们将随机数的性质分为以下三类:
- 随机性: 不存在统计学偏差, 是完全杂乱的数列
- 不可预测性: 不能从过去的数列推测出下一个出现的数
- 不可重现性: 除非将数列本身保存下来, 否则不能重现相同的数列
13 PGP (密码技术的完美组合)
14 SSL/TLS (为了更安全的通信)
15 密码技术与现实社会 (我们生活在不完美的安全中)
附录 A 椭圆曲线密码
附录 B 密码技术综合测验